Page 27 - needle bearings

Calculation of Bearing Loads
NTN

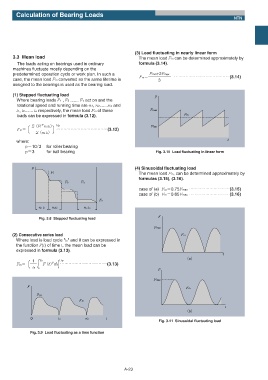
(3) Load fluctuating in nearly linear form
3.3 Mean load The mean load Fm can be determined approximately by
The loads acting on bearings used in ordinary formula (3.14).
machines fluctuate mostly depending on the
predetermined operation cycle or work plan. In such a Fmin 2Fmax
Fmʹʕʕʕʕʕʕʕ ʜʜʜʜʜʜʜʜʜʜʜʜʜ(3.14)
case, the mean load Fm converted so the same lifetime is 3
assigned to the bearings is used as the bearing load.

(1) Stepped fluctuating load
F
Where bearing loads F1 , F2 ....... Fn act on and the
rotational speed and running time are n1, n2.......nn and
t1, t2....... tn respectively, the mean load Fm of these Fmax
loads can be expressed in formula (3.12). Fm
p
ЄʢFi ni tiʣ 1 p Fmin
ʤ Єʢni tiʣ ʥ
Fmʹ ʕʕʕʕʕʕʕ ʜʜʜʜʜʜʜʜʜʜʜʜ(3.12)
where: t
pʹ10 3 for roller bearing
pʹ3 for ball bearing Fig. 3.10 Load fluctuating in linear form

F (4) Sinusoidal fluctuating load
The mean load Fm, can be determined approximately by
F1
formulas (3.15), (3.16).
F2 Fm
case of (a) Fmʹ0.75Fmax ʜʜʜʜʜʜʜʜʜʜ(3.15)
case of (b) Fmʹ0.65Fmax ʜʜʜʜʜʜʜʜʜʜ(3.16)
Fn
n1 t1 n2t2 nn tn

F
Fig. 3.8 Stepped fluctuating load
Fmax
(2) Consecutive series load Fm
Where load is load cycle "to" and it can be expressed in
the function F(t) of time t, the mean load can be
expressed in formula (3.13).
t
ʢaʣ
1
p
t0
ʤ ʥ
p
Fmʹ ʕʕ ́ Fʢtʣdt ʜʜʜʜʜʜʜʜʜʜʜ(3.13)
t0 0
F
Fmax
F
Fm
F(t)
Fm
t
ʢbʣ
0 to 2to t
Fig. 3.11 Sinusoidal fluctuating load

Fig. 3.9 Load fluctuating as a time function

A-23